정렬은 주어진 배열이나 요소들을 요소에 대한 비교 연산자에 따라 재배열 하는 것을 말한다. 정렬 알고리즘은 문제의 복잡성을 줄이기 때문에 중요하다.
예를 들어,
- 출력하려는 데이터가 수백개라면 어떤 식으로든 정리하는 편이 보기 좋다.
- 데이터를 정렬하면 O(1)시간만에 k번째로 작은 항목과 k번째로 큰 항목을 알 수 있다.
- 거대한 데이터셋에서 검색하는 것이 쉬워진다. 정렬된 데이터가 있다면 이진 탐색을 사용해 검색할 수 있다.
- 데이터베이스를 정렬하면 쿼리 성능이 향상된다.
- 데이터셋을 정렬하면 패턴, 추세 및 이상을 식별하는데 도움이 된다.
정렬 알고리즘을 사용하면 다음과 같은 장점이 있다.
- 데이터를 정리하여 정보를 더 쉽고 빠르게 검색하고 분석할 수 있다.
- 많은 알고리즘이 정렬된 데이터셋에서 더 효율적으로 작동한다.
- 정렬을 통해 중복된 요소를 제거하여 메모리 사용량을 줄일 수 있다.
하지만 다음과 같은 단점도 있다.
- 데이터를 정렬된 상태로 유지하기 위해 데이터 삽입 작업에 비용이 많이 든다.
- 주어진 데이터셋에 가장 적합한 정렬 알고리즘을 선택하는데 어려움을 겪을 수 있다.
- 정렬보다 해싱이 더 잘 작동하는 경우가 있다.
기본적인 정렬방법을 몇가지 알아보고 직접 구현해보자.
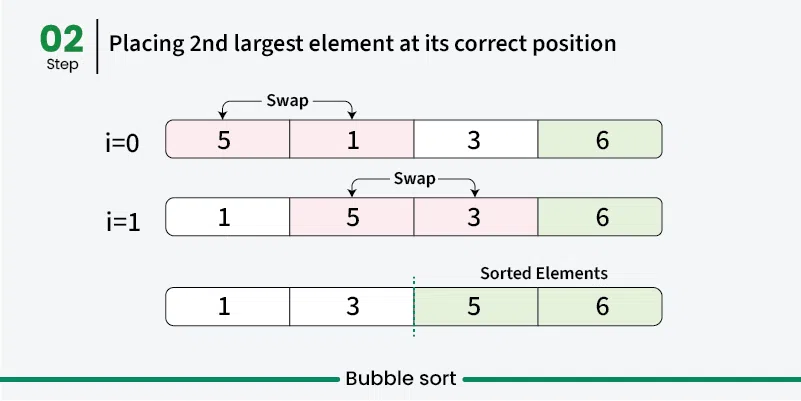
버블 정렬(Bubble Sort)
버블 정렬은 인접한 요소를 반복적으로 비교하여 순서가 잘못되었다면 서로 교체하는 방식의 가장 간단한 정렬 알고리즘이다. 이 알고리즘은 시간복잡도가 매우 크기 때문에 대규모 데이터셋에는 적합하지 않다.


function BubbleSort(arr){
var i, j;
for(i = 0; i < arr.length - 1; i++){
for(j = 0; j < arr.length - i; j++){
if(arr[j] > arr[j + 1]){
[arr[j + 1], arr[j]] = [arr[j], arr[j + 1]];
}
}
}
}버블 정렬의 시간복잡도는 O(n^2)이다.
버블 정렬은 간단한 알고리즘으로, 이해하고 구현하기 쉽다. 또 추가 메모리 공간이 필요하지 않다는 장점이 있다.
하지만 시간복잡도가 크기 때문에 대규모 데이터셋에서는 매우 느리다.
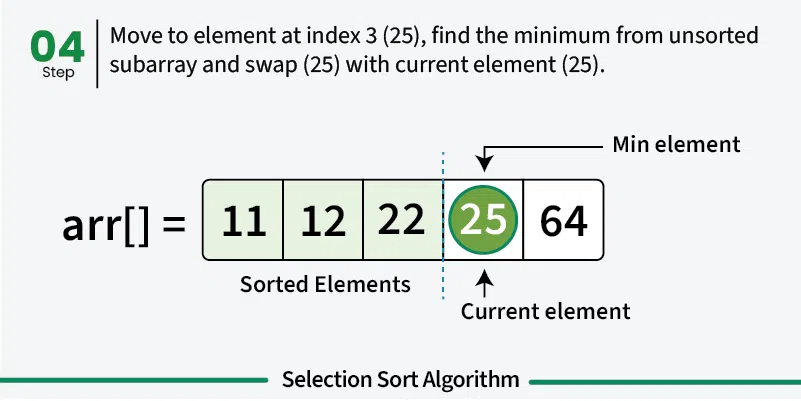
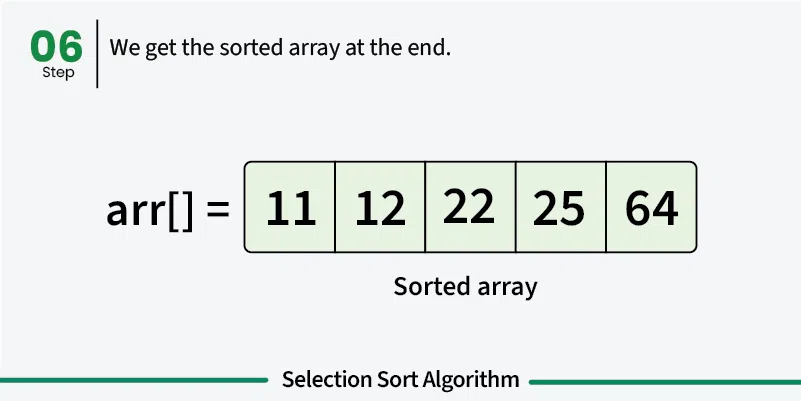
선택 정렬(Selection Sort)
선택 정렬은 정렬되지 않은 부분에서 가장 작은 요소를 반복적으로 선택하여 정렬되지 않은 첫 번째 요소와 위치를 바꾸는 방식으로 정렬한다.




function SelectionSort(arr){
for(var i = 0; i < arr.length - 1; i++){
var min = i;
for(var j = i + 1; j < arr.length; j++){
if(arr[j] < arr[min]){
min = j;
}
}
[arr[i], arr[min]] = [arr[min], arr[i]];
}
}선택 정렬의 시간복잡도는 O(n^2)이다.
선택 정렬도 이해하고 구현하기 쉽고, 추가 메모리 공간이 필요하지 않다. 다른 정렬 알고리즘들에 비해 스왑 횟수가 적다.
하지만 시간복잡도가 크기 때문에 대규모 데이터셋에서는 매우 느리다.
삽입 정렬(Insertion Sort)
삽입 정렬은 정렬되지 않은 목록의 각 요소를 정렬된 목록의 올바른 위치에 반복적으로 삽입하는 방식의 정렬 알고리즘이다. 카드 게임을 할 때 손패를 정리하는 방식과 같다.

function InsertionSort(arr){
for(var i = 1; i < arr.length; i++){
var key = arr[i];
var j = i - 1;
while(j >= 0 && arr[j] > key){
arr[j + 1] = arr[i];
j = j - 1;
}
arr[j + 1] = key;
}
}삽입 정렬의 시간복잡도는 최선의 경우(이미 정렬되어 있는 경우) O(n)으로 매우 빠르지만 평균적으로는 O(n^2)이다.
삽입 정렬도 간단하고 구현하기 쉽다. 이미 정렬되어 있는 데이터셋에서 효율적이다.
하지만 스왑 횟수가 많기 때문에 다른 정렬 알고리즘에 비해 효율적이지 않다.
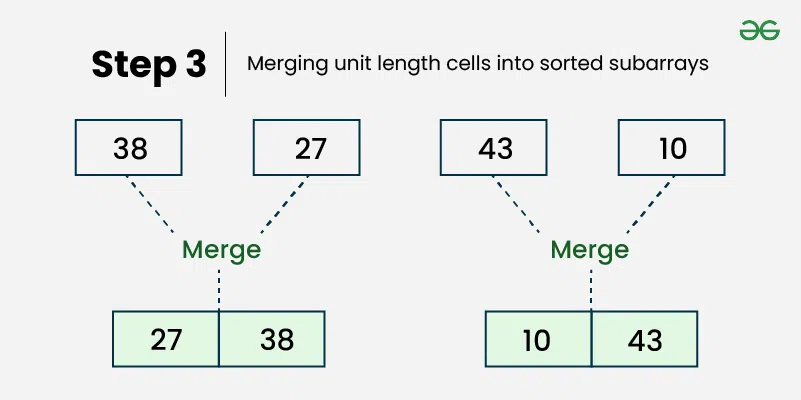
병합 정렬(Merge Sort)
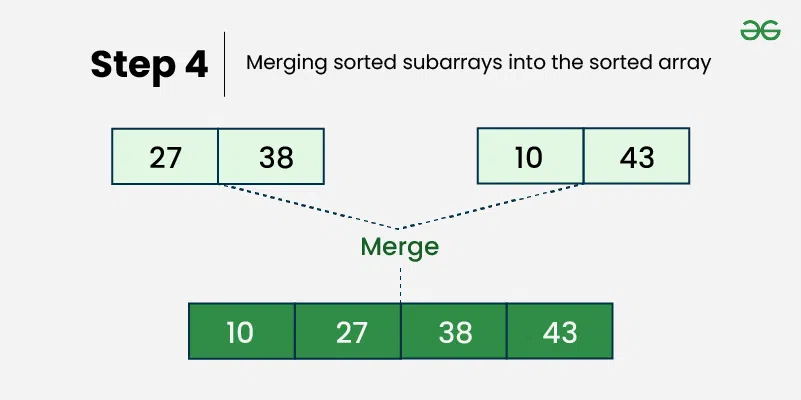
병합 정렬은 분할 정복(Divide and Conquer) 방법을 사용하는 정렬 알고리즘이다. 입력 배열을 더 작은 하위 배열로 나누고 재귀적으로 정렬한 다음 다시 병합한다.


function merge(arr, left, mid, right){
const n1 = mid - left + 1;
const n2 = right - mid;
const L = new Array(n1);
const R = new Array(n2);
for(var i = 0; i < n1; i++)
L[i] = arr[left + i];
for(var j = 0; j < n2; j++)
R[j] = arr[mid + 1 + j];
var i = 0, j = 0;
var k = left;
while(i < n1 && j < n2){
if(L[i] <= R[j]){
arr[k] = L[i];
i++;
}else{
arr[k] = R[j];
j++;
}
k++;
}
while(i < n1){
arr[k] = L[i];
i++;
k++;
}
while(j < n2){
arr[k] = R[j];
j++;
k++;
}
}병합 정렬의 시간복잡도는 O(n log n)으로 위의 다른 정렬들보다 작다.
병합 정렬은 최악의 경우에도 O(n log n)의 시간복잡도를 가지므로 대규모 데이터셋에서도 좋은 성능을 보여준다.
하지만 재귀적인 분할정복 방식으로 추가적인 메모리가 필요하다.
퀵 정렬(Quick Sort)
퀵 정렬은 분할 정복 방식을 사용하는 정렬 알고리즘이다. 어떤 요소를 피벗으로 선택하고, 선택한 피벗을 중심으로 주어진 배열을 분할하여 정렬하고, 피벗을 올바른 위치에 배치한다.

퀵 정렬에서 피벗을 선택하는 다양한 방법이 있다.
- 첫 번째 또는 마지막 요소를 피벗으로 선택하는 경우 배열이 이미 정렬되어 있는 경우 최악의 경우로 끝난다.
- 임의의 요소를 피벗으로 선택하는 경우 최악의 경우가 발생하는 패턴이 없기 때문에 선호된다.
- 중간의 요소를 피벗으로 선택하는 경우 시간복잡도 측면에서는 최선이지만 중간을 찾는 과정때문에 평균적으로는 더 많은 시간이 걸린다.
function partition(arr, low, high){
let pivot = arr[high];
let i = low - 1;
for (let j = low; j <= high - 1; j++) {
if (arr[j] < pivot) {
i++;
swap(arr, i, j);
}
}
swap(arr, i + 1, high);
return i + 1;
}
function swap(arr, i, j){
let temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
function quickSort(arr, low, high)
{
if (low < high) {
let pi = partition(arr, low, high);
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}퀵 정렬의 시간복잡도는 최선의 경우 Ω(n log n), 평균적 경우 θ(n log n), 최악의 경우 O(n²)이다.
퀵 정렬은 시간복잡도가 작기 때문에 대규모 데이터셋에 적합하다. 그리고 메모리도 많이 필요하지 않다. 게다가 배열을 복사하지 않기 때문에 캐시 친화적이다.
하지만 피벗을 잘못 선택할 경우 최악의 시간복잡도가 나타날 수 있다.
힙 정렬(Heap Sort)
힙 정렬은 이진 힙 데이토 구조에 기반한 정렬 알고리즘이다. 선택 정렬에 대한 최적화로 볼 수 있는데, 먼저 최대 요소를 찾아서 마지막 요소와 바꾼다. 나머지 요소에 대해서도 같은 과정을 반복한다.
힙 정렬을 위해서는 먼저 입력된 배열을 heapify를 사용하여 배열을 최대 힙으로 변환해야한다. 배열은 힙 속성을 가지도록 다시 정렬된다. 그런 다음 힙에서 루트 노드를 하나씩 배열의 마지막 노드와 스왑하면서 heapify한다.
먼저 입력된 배열을 이진트리로 만든다.

그 다음 구성된 힙을 최대 힙으로 만든다.
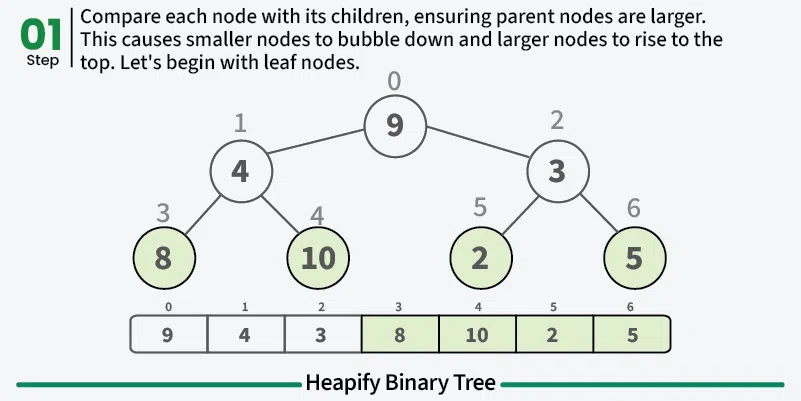


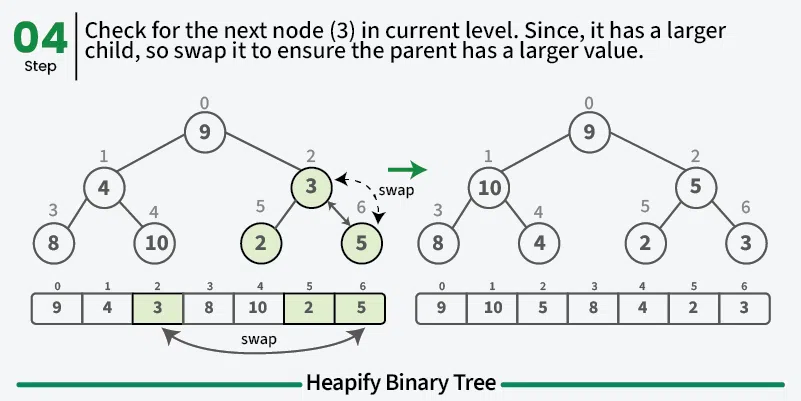



이제 루트 힙이 빌때까지 루트 노드를 빼서 배열의 마지막 노드와 스왑한다.






// 트리를 heapify한다.
function heapify(arr, n, i) {
var largest = i;
var left = 2 * i + 1;
var right = 2 * i + 2;
// If left child is larger than root
if (left < n && arr[l] > arr[largest]) {
largest = left;
}
// If right child is larger than largest so far
if (right < n && arr[r] > arr[largest]) {
largest = right;
}
// If largest is not root
if (largest !== i) {
[arr[i], arr[largest]] = [arr[largest], arr[i]];
// Recursively heapify the affected sub-tree
heapify(arr, n, largest);
}
}
function heapSort(arr) {
var n = arr.length;
// Build heap (rearrange array)
for (var i = Math.floor(n / 2) - 1; i >= 0; i--) {
heapify(arr, n, i);
}
// One by one extract an element from heap
for (var i = n - 1; i > 0; i--) {
// Move current root to end
[arr[0], arr[i]] = [arr[i], arr[0]];
// Call max heapify on the reduced heap
heapify(arr, i, 0);
}
}힙 정렬의 시간복잡도는 O(n log n)이다. 시간복잡도는 퀵 정렬과 같지만 잘 구현된 퀵 정렬에 비해 2~3배 정도 느리다. 캐시 친화적이지 않기 때문이다.
힙 정렬은 모든 경우에 O(n log n)의 시간복잡도를 가지기 때문에 일관적인 효율을 보인다. 또 메모리 사용을 최소화할 수 있다. 재귀와 같은 방식을 사용하지 않기 때문에 이해하기가 더 간단하다.
'CS > 알고리즘' 카테고리의 다른 글
| Array, Linked List (0) | 2025.02.26 |
|---|---|
| DFS, BFS (0) | 2025.02.24 |
| Big-O (0) | 2025.02.17 |